[자료구조] 그래프
Graph (그래프)
그래프란?
그래프: 정점(vertex)과 간선(edge)으로 이뤄진 비선형 자료구조.
현실 세계의 사물, 객체, 추상적인 개념 간의 연결 관계를 표현한 것그래프는 정점(Vertex, node)과 간선(edge)으로 이뤄진 비선형 자료구조이며 정점과 간선들의 유한 집합이라고 할 수 있다.
e.g. 도시들을 연결하는 도로망, 사람들의 지인 관계, 네트워크, 웹 사이트 간의 링크 관계 그래프에는 부모 자식 관계에 대한 제약이 없기 때문에, 트리보다 훨씬 다양한 구조를 표현할 수 있고 그만큼 많은 문제를 해결하는데 쓰일 수 있다. 그래프는 정점들과 간선들로 정의되며, 정점의 위치 정보나 간선의 순서는 그래프를 정의하는 요소가 될 수 없다.
그래프의 종류
그래프의 정점과 간선에는 추가적인 속성을 부여할 수 있고, 형태에 제약을 둘 수 있다. 그에 따라 종류가 나뉘어진다.
방향 그래프 (directed graph)
각 간선이 방향 속성을 갖는 그래프.
짝사랑 관계, 도로망의 일방통행 등을 표현할 수 있다.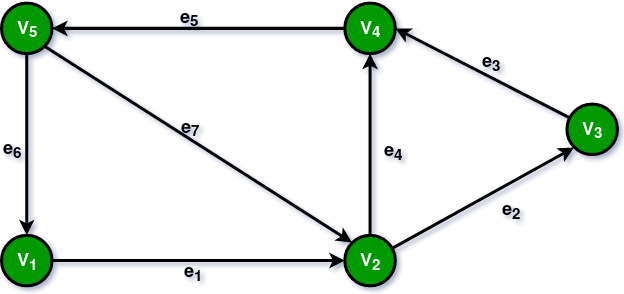
방향은 경로에 있어서 중요한 속성이 된다.
예를 들어 위 그림에서 V3에서 V2로 가려면, e2간선을 쓰지 못하고 e3, e5, e7을 거쳐야 한다.
반대로 방향 속성을 갖지 않는 그래프를 무향 그래프(undirected graph)라고 부른다.
가중치 그래프 (weighted graph, network)
각 간선이 가중치 속성을 갖는 그래프.
이 속성은 두 도시 사이의 거리, 두 외화 사이의 환율, 두 사람 사이의 호감도 등을 표현할 수 있다.
가중치 그래프는 네트워크라고도 부르며, 최소 신장 트리, 최단 경로 알고리즘에 쓰인다.
다중 그래프와 단순 그래프 (multi graph and simple graph)
두 정점 사이에 두 개 이상의 간선이 있을 수 있는 그래프.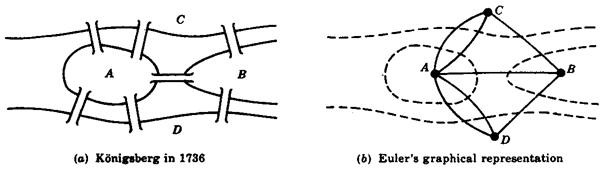
위 그림은 그래프 이론의 시초인 오일러의 쾨니히스베르크 다리 그림이다.
각 지면을 정점, 다리를 간선이라고 보면 하나의 그래프가 생기고, 이는 다중 그래프다.
반대로 두 정점 사이에 딱 하나의 간선만이 있는 그래프를 단순 그래프라고 부른다.
그래프의 용어
간선(u,v): 정점u에서 정점v를 잇는 선. 간선은 무게/값/비용 등의 가치를 가질 수 있다.경로(path): 정점과 정점 사이에 연결된 간선들을 순서대로 나열한 것이다. (대부분 한 정점을 한번만 지나는 경로인단순 경로(simple path)를 의미)부분 그래프(subgraph): 어떤 그래프의 정점의 일부와 간선의 일부로 이뤄진 또 다른 그래프인접 정점(adjacent vertex)란 간선에 의해 한 정점과 직접 연결된 정점정점의 차수(degree): 한 정점에 인접한 정점의 수(=정점에 그어진 간선의 수). 방향 그래프에서는 외부로 향하는 간선의 개수를진출 차수, 외부로부터 오는 간선의 개수를진입 차수라고 부른다.사이클(cycle): 시작 정점과 종료 정점이 동일한 (단순)경로. 트리는 그래프의 특수한 형태로서, 사이클을 갖지 않는 그래프다.
그래프 구현
그래프는 트리와는 달리 새로운 정점이나 간선을 추가,삭제할 일이 별로 없다.
따라서 대부분의 그래프는 구조의 변경이 어렵더라도 간단하고 메모리를 적게 차지하는 정적인 방법으로 구현된다.
그래프의 정점들을 하나하나 객체 인스턴스로 표현하는 대신,
각 정점에 0부터 시작하는 번호(index)를 붙이고 배열에 각 정점의 정보를 저장한다.
그래프 표현은 간선의 정보를 어떤 식으로 저장하느냐에 따라 크게 두가지로 나뉜다.
인접 리스트(adjacency list)
인접 리스트 표현 방법에서는 그래프의 각 정점마다 해당 정점에서 나가는 간선들의 목록을 저장해서 표현한다. (array of linked list)
즉, 각 정점마다 하나의 연결 리스트를 갖는다. 여기서 주의할 점은, 이건 어떤 경로를 나타내는게 아니라 말 그대로 각 정점의 인접 정점들을 나열한다는 것.
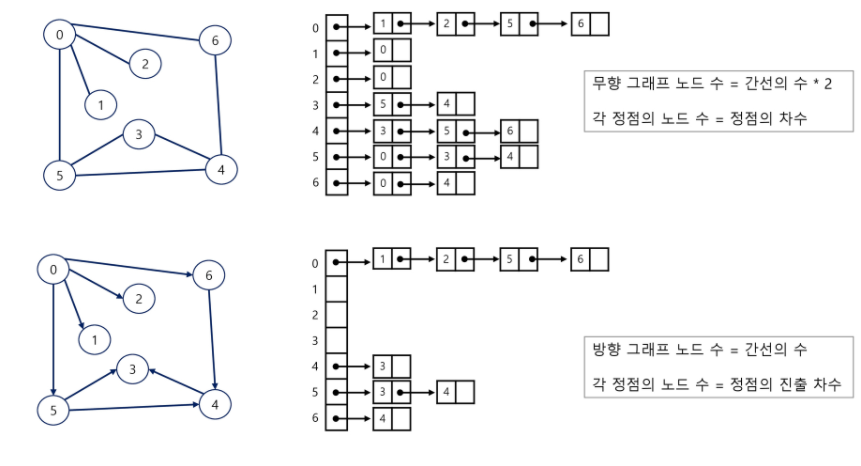
인접 리스트 구현 (c++)
c++
vector<list<int>> adj; // adj[i]는 정점 i와 연결된 정점들의 번호를 저장하는 연결리스트.
// add edge (u,v)
adj[u].insert(v);
adj[v].insert(u);
인접 행렬(adjacency matrix)
인접 리스트 표현의 단점 : 두 정점이 주어질 때 둘의 연결 여부를 알기 위해선 한쪽 정점에 달린 연결 리스트를 일일이 뒤져야 한다
특정 간선의 존재 여부 혹은 가중치 값에 접근하기 빠르게 하기 위해 인접 행렬 표현을 쓴다.
V * V 크기의 2차원 배열을 이용한다.
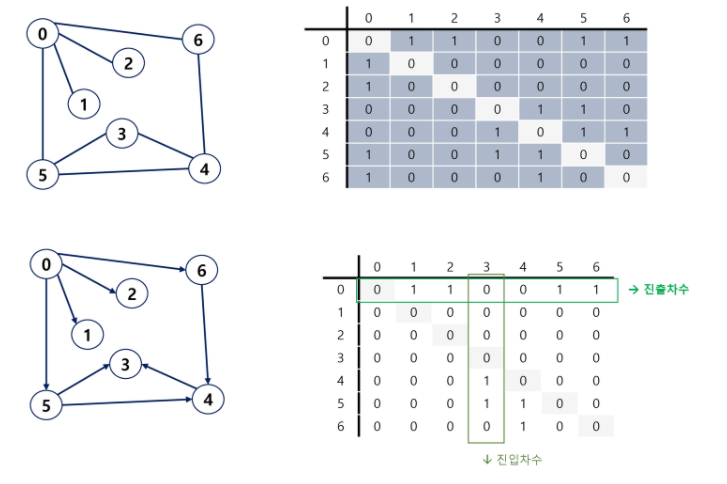
인접 행렬 구현 (c++)
c++
vector<vector<bool>> adj; // 가중치 없는 가장 간단한 형태의 그래프(간선이 있으면 1, 없으면 0)
// add edge(u,v)
adj[u][v] = 1;
인접 행렬 표현의 단점 : 실제 간선의 개수와 상관없이 항상 O(V^2) 크기의 공간을 사용해야 한다.
반면 인접 리스트 표현은 연결리스트에 실제 간선 수만큼만 원소가 들어있으므로 O(V + E) 공간만 쓰면 된다.
희소 그래프(sparse graph): 간선의 수가 V^2에 비해 훨씬 적은 그래프밀집 그래프(dense graph): 간선의 수가 V^2에 거의 비례하는 그래프
인접 리스트 표현은 희소 그래프, 인접 행렬 표현은 밀집 그래프를 표현할 때 각각 유리하다.
인접 리스트 vs 인접 행렬
V = 정점의 개수, E = 간선의 개수, degree(V) = 정점의 차수
| 인접 행렬(Adjacency Matrix) | 인접 리스트(Adjacency List) | |
| 공간 | V^2 | V+E |
| 간선 (u,v) 검색 | O(1) : 2차원 배열의 원소 접근 연산. matrix[i][j] | O(degree(V)) : 한 정점의 연결리스트를 탐색. |
| 정점 추가 | O(V^2) : 배열 크기가 (V+1)^2로 증가시키는 중의 배열 복사 비용. | O(1) 원소 하나만 추가하면 끝 |
| 간선 추가 | O(1) matrix[i][j] = 1 | O(1) 리스트에 추가하면 끝 |
| 정점 삭제 | O(V^2) 배열 크기가 (V-1)^2로 감소하기 때문에 배열 복사 비용 생김. | O(V+E) 삭제한 공간을 채우기 위해 나머지 원소들을 shift해야 하고, 다른 정점의 연결리스트에서 삭제된 정점을 찾아 삭제 |
| 간선 삭제 | O(1) matrix[i][j] = 0 | O(E) 정점의 연결리스트에서 인접 정점 검색하는 시간 및 삭제 시간 |
인접 행렬은 간선 검색, 추가, 삭제에 강하기 때문에 정점의 갯수가 고정적이라면 인접행렬이 훨씬 빠르다.
반면 인접 리스트는 정점 추가, 삭제에 강하기 때문에 간선의 갯수가 고정적이라면 인접 리스트가 빠르다.
둘 다 고정적이라고 한다면, 밀집 그래프엔 인접 행렬(검색 시간이 빠르기 때문에)을 쓰고 희소 그래프에는 인접 리스트(공간을 아끼기 위해)를 쓰는 것이 좋다.